Научный журнал

Научное обозрение. Экономические науки

ISSN 2500-3410

ПИ №ФС77-57503

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Щипицын А.Г. 1

---

1 ГОУ ВПО «Национальный исследовательский Южно-Уральский государственный университет» Минобразования России

Рассматриваемый подход основан на критерии: удельные веса валют стран должны быть поставлены в соответствие с относительными показателями материальных ценностей стран. В соответствие с этим критерием выполнено математическое описание, составлен алгоритм и разработан программный модуль, на вход которого вводится информация о численных значениях компонент исходных материальных ценностей стран, накопленных к некоторому моменту времени, весовых коэффициентах значимости этих компонент, а выводится информация об относительных показателях материальных ценностей, на основе которых затем определяются искомые соотношения валют стран.

Статья в формате PDF

0 KB

материальные ценности

относительный показатель

весовые коэффициенты

соотношения валют стран

алгоритм

программный модуль

1. Людвиг фон Мизес. Человеческая деятельность: Трактат по экономической теории [Текст] – М.: Социум, 2012. – 880 с.

2. Мюррей Ротбард. Государство и деньги: как государство завладело денежной системой общества// Пер. с англ. и франц.[Текст] – М.: Социум, 2008. – 207 с.

3. Щербинин Ю.А., ред. Мировая экономика: Учебник для вузов [Текст] – М.: ЮНИТИ-ДАНА, 2004. – 318 с.

4. Гришина О.А., Звонова Е.А. Регулирование мирового финансового рынка: Теория, практика, инструменты [Текст] — М.: ИНФРА-М, 2010. — 410 с.

5. Валютный курс. Википедия. [Электронный ресурс] // Режим доступа: https://ru.wikipedia.org/wiki/

6. Фиксинг Ротшильда [Электронный ресурс] // Режим доступа: http://dokumentika.org/bilderbergskiy-klub/fiksing-rotshilda

7. Краткий курс: Концепция общественной безопасности [Электронный ресурс] // С-Петербург, 2004. — 563 с. – Режим доступа: http://kobtv.narod.ru/files/Knigi-KOB/Kratkiy-kurs.pdf

8. Кризис глобальной финансовой системы [Электронный ресурс] //Семинар в С-Петербурге 23.12.2014. – Режим доступа: http://kobtv.narod.ru/lector/seminar-krizis-globalnoi-finansovoi-sistemy.html

9. Список стран по населению. Википедия [Электронный ресурс] // Режим доступа: http://ru.wikipedia.org/wiki

10. Площадь стран мира. Википедия [Электронный ресурс] // Режим доступа: http://ostranah.ru/_lists/area.php

11. Список стран по производству электроэнергии. Википедия [Электронный ресурс] // Режим доступа: http://ru.wikipedia.org/wiki

12. Список стран по экспорту. Википедия. [Электронный ресурс] // Режим доступа: http://ru.wikipedia.org/wiki/

13. Список стран по ВВП (номинал). Википедия [Электронный ресурс] // Режим доступа: http://ru.wikipedia.org/wiki

14. Список стран по ожидаемой продолжительности жизни. Википедия [Электронный ресурс] // Режим доступа: http://ru.wikipedia.org/wiki

15. Щипицын А.Г. Программный модуль анализа адекватности подхода к определению соотношений валют стран мира // Свидетельство о регистрации электронного ресурса № 21562 от 22.12.2015. Реферат опубликован в газете «Хроники объединённого фонда электронных ресурсов «Наука и образование»», № 12 (декабрь), 2015. – С. 47.

Рассматриваемый подход основан на постулате: чем богаче страна реальными материальными ценностями (МЦ), тем весомее должна быть её валюта. Этот постулат озвучил ещё А.С. Пушкин в седьмой строфе первой главы поэмы «Евгений Онегин»: «…И был глубокий эконом, то есть умел судить о том, как государство богатеет и чем живёт, и почему не нужно золота ему, когда простой продукт имеет…». Другими словами, удельный вес валюты страны должен быть поставлен во взаимно-однозначное соответствие с относительным показателем материальных ценностей (ОПМЦ) страны. Это обстоятельство является существенным условием справедливого жизнеустройства стран мира.

Математическое описание

ОПМЦ страны складывается из накопленных и потенциальных величин МЦ в заданные моменты времени внутри некоторого интервала времени и определяется списком показателей, в каждую позицию которого вложен список компонент первого уровня, в каждую позицию списка компонент первого уровня вложен список компонент второго уровня и так далее. Числовые данные по каждой позиции списка компонент последнего уровня вложенности характеризуют исходные абсолютные значения МЦ страны. Путём суммирования одноимённых исходных абсолютных значений МЦ в единой размерности каждой страны определяются мировые абсолютные значения МЦ по каждой позиции списка компонент последнего уровня вложенности, то есть определяются мировые исходные абсолютные величины МЦ. Далее путём деления абсолютных величин МЦ компонент страны последнего уровня вложенности на соответствующие мировые абсолютные значения МЦ компонент последнего уровня вложенности определяются относительные исходные величины МЦ страны. Затем определяются относительные величины компонент МЦ предпоследнего уровня вложенности страны путём суммирования произведений относительных исходных величин компонент МЦ этой страны на соответствующие весовые коэффициенты, процедура вычисления которых будет пояснена ниже. После этого аналогично определяются относительные величины компонент МЦ страны пред-предпоследнего уровня вложенности и так далее, до первого уровня вложенности, а затем и определения искомых ОПМЦ страны, как произведений относительных величин компонент МЦ страны первого уровня вложенности на соответствующие весовые коэффициенты страны и усреднения этих величин на рассматриваемом интервале времени. Список компонент по каждому уровню вложенности составляется в порядке убывания значимости компоненты МЦ для богатства страны. Критерий «убывания значимости» является субъективным, но: 1) он должен быть единым для всех стран мира и 2) должен быть определён на основе договорного нравственного произвола компетентных представителей всех стран мира, которые владеют информацией о значимости той или иной МЦ для пополнения мирового богатства. То есть иерархически упорядоченные списки компонент и показателей МЦ составляются с учётом указанных замечаний. Весовой коэффициент по каждой позиции каждого списка компонент МЦ страны определяется в зависимости от номера позиции этой компоненты в таком списке и удовлетворяет условиям: 1) чем меньше номер, тем больше весовой коэффициент, 2) сумма весовых коэффициентов по каждой позиции для одного списка равна единице.

Поясним сказанное в символах для одного уровня вложенности. Введём обозначения:

NC – количество стран в списке для определения соотношения валют (в частности, это количество стран в мире);

N0 – количество показателей МЦ страны;

N1 – количество компонент в показателе МЦ страны;

Qkij – абсолютное исходное значение МЦ по компоненте j показателя i страны k в размерности этой МЦ, где здесь и далее индексы k = 1,…,NC; i = 1,… N0; j = 1,…, N1;

ckij – весовой коэффициент для относительной величины компоненты МЦ номер j показателя номер i страны номер k;

cki – весовой коэффициент для относительного показателя МЦ номер i страны номер k;

ck – весовой коэффициент для страны номер k.

Можно показать, что, для удовлетворения весовыми коэффициентами указанным выше условиям следует использовать формулы:

ckij = (1/j)/S1, j=1,…, N1, (1)

где

S1 = 1/1 + 1/2 +1/3 + … +1/N1; (2)

cki = (1/i)/S0, i =1,… N0, (3)

где

S0 = 1/1 + 1/2 +1/3 + … +1/N0; (4)

ck = (1/k)/Sc, (5)

где

Sc =1/1 + 1/2 +1/3 + … +1/Nc. (6)

Алгоритм

0: составить иерархически упорядоченные списки (по убыванию уровней значимости) наименований компонент МЦ, показателей МЦ, стран и задать:

t0 – начальный момент времени интервала, в течение которого валюты стран остаются неизменными;

T – конечный момент времени указанного интервала;

NT – количество моментов времени, в которые заданы массивы Qkij;

tn – моменты времени, в которые заданы массивы Qkij, n = 0, 1, 2, …, NT;

Nc – количество стран в списке для определения соотношения валют (в частности, это количество стран в мире);

N0 – количество исходных показателей МЦ страны;

N1 – количество компонент в исходном показателе МЦ;

Qkij(tn) – абсолютные исходные значения МЦ в момент времени tn по компонентам j показателей i стран k в размерностях этих МЦ; k = 1,…, Nc; i=1,…,N0; j=1,…, N1; n = 1,…,NT;

ckij – весовой коэффициент для относительной величины компонент МЦ номер j показателя номер i страны номер k, вычисленный по формулам (1), (2);

cki – весовой коэффициент для относительного показателя МЦ номер i страны номер k, вычисленный по формулам (3), (4);

ck – весовой коэффициент для страны номер k, вычисленный по формулам (5), (6). Далее указаны операции по вычислению для моментов времени tn: суммарных для всех стран абсолютных величин исходных значений МЦ Q0ij(tn), относительных значений для каждой компоненты МЦ каждой страны qkij(tn), средневзвешенных значений для каждого показателя МЦ каждой страны qki(tn), средневзвешенных значений для всех показателей МЦ каждой страны qk(tn), и в конечном итоге – вычисление усреднённых на интервале времени [t0; T] значений ОПМЦ Pk:

1: n = 0; Pk = 0, k = 1,…, Nc;

2: Q0ij(tn) = 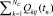, i=1,..,N0; j=1,.., N1; (7)

3: qkij(tn) = Qkij(tn)/Q0ij(tn), k = 1,…, Nc; i=1,…,N0; j=1,…, N1; (8)

4: qki(tn) = 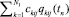, k = 1,…, Nc; i=1,…,N0; (9)

5: qk(tn) = 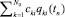, k = 1,…, Nc; (10)

6: pk(tn) = ckqk(tn), k = 1,…, Nc; (11)

7: Pk = Pk + [pk(tn)]/NT; k = 1,…, Nc; (12)

8: n = n +1; (13)

9: если n <= NT, то идти к 2; (14)

10: вывести Pk , k = 1,…, Nc.

Для фиксации массивов исходных данных Qkij(tn) целесообразно заполнить Nc таблиц для каждого момента времени n = 1,…, NT, то есть всего NcхNT таблиц, каждая из которых имеет структуру, показанную ниже. В левой верхней клетке таблицы записывается номер страны. В левом столбце записываются номера показателей. В верхней строке записываются номера компонент показателя. В клетки таблицы записываются числа указанных исходных данных, соответствующие номеру страны (k), номеру показателя (i) и номеру компоненты (j), которые подаются на вход приведённого выше алгоритма, выходом которого являются усреднённые по времени ОПМЦ каждой страны (Pk).

Определив соотношения валют стран, далее следует выбрать единицу валюты, например, приняв за таковую единицу валюты страны, получившей наибольший ОПМЦ. И далее вычислить курсы валют остальных стран через величину валюты, принятой за единицу.

Следует заметить, что среди исходных массивов Qkij(tn) могут быть отрицательные числа, вводимые, в частности, для учёта количественных показателей долга страны перед другими странами, вредных экологических воздействий этой страной на население и природу, а также развязывание страной военных действий в режиме агрессора.

Существенные замечания

Современные информационные технологии позволяют создать мониторинг исходных массивов Qkij(tn), которыми может быть учтено максимальное количество показателей, отражающих имеющиеся материальные ценности стран и их изменение с течением времени. С целью контроля достоверности такого мониторинга имеет смысл создать мировую комиссию из компетентных представителей каждой страны, обладающих человечным типом строя психики с целью минимизировать возможный безнравственный произвол того или иного члена комиссии. Всех без исключения членов этой следует наделить полномочиями доступа к необходимой исходной информации и методам её обработки с целью определения соотношений валют.

Рассмотренный подход позволит, в частности:

1) устранить злонамеренный произвол в определении соотношений валют разных стран, когда валюту одной страны можно «опускать» или «поднимать» в соответствии с корыстным интересом другой страны или группы стран;

2) высветить «прибыль», получаемую группой лиц страны или некоторой страной в целом в результате операций с валютой без соответствующего её материального обеспечения: например, выпуск необеспеченных материальными ценностями денег данной страны, на которые «покупаются» реальные материальные ценности других стран, игрой на понижении или повышении курсов валют и другие подобные процедуры бумажного движения без адекватного материального производства; другими словами: вес валюты страны следует повышать или понижать только при условии соответственно увеличения или уменьшения МЦ этой страны, а следовательно колебания весов валют должны иметь низкочастотный характер во времени.

В научном направлении «Мировая экономика» (например, работы [1] – [5]) уделено внимание методам определения курсов валют, например, на основе: сопоставления цен на золото, уровня цен на стандартный набор товаров и услуг («потребительскую корзину»), соотношений производственных расходов (заработная плата, производительность труда, норма ссудного процента), паритета покупательной способности (для формулирования которого обычно применяют так называемый закон одной цены: цена товара в одной стране должна быть равна цене товара в другой стране; а поскольку эти цены выражаются в разных валютах, это соотношение цен и определяет курс обмена одной валюты на другую) и т.п. Но очень мало информации [6] о критериях, на основе которых разработаны эти методы, а также отсутствует информация об активном участии представителей всех стран в процедуре определения курсов валют.

В фундаментальной работе [7], в частности, теоретически обстоятельно обоснован метод определения курсов валют на основе энергоресурсов страны, а на семинаре [8] доложены результаты по определению соотношений валют стран для двух вариантов: на основе уровня производства электроэнергии странами мира и на основе уровня потребления электроэнергии ими этими странами.

В данной работе, а именно в приведённой выше методике составления алгоритма и в алгоритме вычисления ОПМЦ, учитываются и эти подходы определения соотношений валют, как вложения в этот алгоритм. Следует заметить, что приведённый алгоритм может быть усложнён введением любого количества уровней вложенности компонент, а также упрощён путём ограничений на количество показателей и снятием уровней вложенности компонент показателей. Но следует также заметить, что указанные усложнения и упрощения алгоритма всегда будут отражать определённый произвол «методологов», который может быть как нравственным, так и безнравственным. Это же замечание относится и к назначению указанных выше весовых коэффициентов, которыми может быть выделена значимость того или иного показателя материальных ценностей.

В качестве примера приведём небольшой перечень показателей (обозначены одним числом) и их компонент первого уровня вложенности (обозначены двумя числами, отделёнными точкой):

1.Территория страны

1.1. Общая площадь

1.2. Площадь лесов

1.3. Площадь морей, озёр и рек

1.4. Площадь равнин

1.5. Площадь гор

2. Природные ресурсы

2.1. Внутри земли: нефть, газ, уголь, цветные металлы, руда чёрных металлов и т.п.

2.2. Внутри воды: рыба, водоросли и т.п.

2.3. На поверхности земли: деревья, злаки, травы и т.п.

3. Население

3.1. Общая численность

3.2. Средняя продолжительность жизни

3.3. Численность занятых производительным трудом

3.4. Численность обучающихся для производительного труда

4. Инфраструктура

4.1. Производство электроэнергии

4.2. Производственная недвижимость

4.3. Бытовая недвижимость

4.4. Техника транспорта и связи

4.5. Военная техника

5. Продукция

5.1. Внутренний валовый продукт

5.2. Промышленная продукция

5.3. Сельскохозяйственная продукция

5.4. Продукция сферы услуг

5.5. Бытовая продукция

5.6. Импортируемая продукция

5.7. Экспортируемая продукция

Числовой пример

Исключительно для пояснения метода вычислений по алгоритму рассмотрим простейший пример определения соотношения валют нескольких стран на основе исходной числовой информация [9] – [14], имеющейся в открытом доступе. Количество стран Nc = 9, иерархический упорядоченный список которых по численности населения следующий: 1) КНР, 2) Индия, 3) США, 4) Россия, 5) Япония, 6) Германия, 7) Великобритания, 8) Франция, 9) Швейцария. Общая численность населения перечисленных стран – это, примерно, половина численности населения Земли. Ограничим вычисления только показателями (без вложенных компонент), иерархически упорядоченный список которых по субъективному критерию значимости следующий: 1) численность населения (млн. чел.), 2) площадь (км2), 3) производство электроэнергии (Гвт*ч), 4) экспорт (млн. долл. США), 5) внутренний валовый продукт по номиналу (млрд. долл. США), 6) средняя продолжительность жизни (годы), В данном случае составляем одну таблицу, в левом столбце которой записаны указанные страны, в её верхней строке перечислены наименования указанных показателей с указанием размерностей соответствующих чисел, а во внутренних клетках записаны соответствующие величины показателей.

В обозначениях приведённого выше алгоритма для этого примера имеем: Nc = 9, N0 = 6, Qki – это массив размера 9х6, величины компонент которого заданы в приведённой выше таблице в столбцах, пронумерованных с 1 по 6. Весовые коэффициенты cki вычисляются по формулам (3), (4), а весовые коэффициенты ck вычисляются по формулам (5), (6). Далее используются формулы (7) – (11) алгоритма при условии отсутствия компонент первого уровня вложенности и изменения показателей во времени. С учётом этих ограничений из алгоритма (7) – (11) выпадают пункты 4, 7, 8, 9 и усечённый алгоритм имеет вид:

2: Q0i = 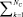Qki, i=1,…,N0;

3: qki = Qki/Q0i , k = 1,…, Nc; i=1,…,N0;

5: qk = 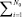cki qki, k = 1,…, Nc;

6: pk = ckqk(tn), k = 1,…, Nc;

10: вывести pk , k = 1,…, Nc.

Результаты вычислений по этому алгоритму приводят к следующим значениям ОПМЦ в данном примере для блока из девяти стран:

p1 = 0,110301, p2 = O,033885, p3 = 0,021345, p4 = 0,011709 , p5 = 0,003682 , p6 = 0,002935 , p7 =0,001577 , p8 = 0,001570 , p9 = 0,0005548 .

Определив наибольшее значение из этих величин p0 = 0,110301и номер страны, которая имеет это наибольшее значение – это k = 1, принимаем за единицу «мировой» валюты (а в данном частном случае её следовало бы назвать «блочной» валютой для блока из девяти стран) единицу валюты этой страны. И наконец, определяем коэффициенты пересчёта валют стран через единицу «мировой» валюты по формуле hk = pk/p0 , k = 1,…, Nc, численные значения которых для данного примера таковы:

h1 = 1,000000, h2 = 0,307213, h3 = 0,193515, h4 = 0,106151, h5 = 0,033378, h6 = 0,026607, h7 = 0,014294, h8 = 0,014232, h9 = 0,004968.

На основе этих чисел следует устанавливать курс валюты каждой страны, который поставлен в соответствие с относительным показателем материальных ценностей этой страны.

О программе

На основе алгоритма (7) – (11) разработан программный модуль [15], на вход которого подаётся информация по пункту 0, а выводится информация по пункту 10. Программный модуль позволяет проводить численное моделирование с целью исследования, в частности, влияния субъективизма в составлении иерархически упорядоченных списков значимости исходных МЦ на соотношения валют стран. На основе этого программного модуля может быть разработана программа определения соотношения валют при необходимом количестве показателей, с необходимым количеством компонент по каждому показателю и при необходимом количестве уровней вложенности компонент. А в целом разработанная указанным образом программа может служить инструментом поддержки приятия решений о возможности практического использования предлагаемого подхода определения соотношений валют стран.

Библиографическая ссылка