science-review.ru
Введение
Уравнение модели Харрода-Домара с экзогенной динамикой потребления произвольного характера – это дифференциальное уравнение первого порядка, в котором независимой переменной является время, а доход рассматривается, как сумма потребления и инвестиций [13, 15]. Основная предпосылка [2, с. 205] состоит в пропорциональности инвестиций и производной по времени от дохода с множителем, называемым коэффициентом капиталоемкости прироста дохода. До некоторых пор считалось, что этот коэффициент постоянен [2, 14], потому что решение дифференциального уравнения для этого случая известно [15, 9]. Однако, благодаря результатам работ [10, 11, 12] появилась возможность предположить, что коэффициент капиталоемкости прироста дохода есть переменная функция достаточно произвольного характера. Кроме этого, поставлена и решена задача оптимального управления, как задача максимизации интегральной дисконтированной полезности потребления [5], которая до результатов работ [10, 11, 12] могла быть решена лишь в случае постоянного коэффициента приростной капиталоемкости [1].
Модель макроэкономической динамики Солоу весьма популярна и уже стала классической в математической экономике [15, 3, 4, 16]. Уравнение модели макроэкономической динамики Солоу с переменными коэффициентами хорошо известно [3] – это дифференциальное уравнение первого порядка, и в котором независимой переменной является время, а искомой функцией является фондовооруженность. Модель Солоу сложнее предыдущей модели Харрода-Домара, т. к. сложнее именно это дифференциальное уравнение. Задача Коши для него лишь сводится к интегральному уравнению [7, 8]. Однако, несмотря на это усложнение по сравнению с предыдущей моделью, задача оптимального управления и в этой модели ставится, как максимизация интегральной дисконтированной полезности среднедушевого потребления [6], которая в этой же работе успешно решена.
Особенности вариационного метода решения задачи оптимизации потребления модели экономической динамики Харрода-Домара
Уравнение модели Харрода-Домара с экзогенной динамикой потребления произвольного характера [13, 15] имеет вид
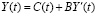(1.1).
Здесь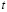 
– время, 
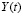– доход, который рассматривается, как сумма потребления 
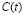и инвестиций 
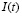. Основная предпосылка [2, с. 205]:
,
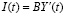где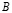 
– коэффициент капиталоемкости прироста дохода.
До некоторых пор считалось, что [14]
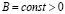. (1.2)
Для случая (1.2) решение дифференциального уравнения (1.1) известно [9] и дается формулой
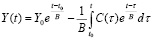. (1.3)
Здесь предполагаются выполненными начальные условия
, 
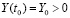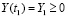. (1.4)
В работах [10, 11, 12] делается наиболее общее предположение
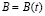. (1.5)
При условиях (1.4) и (1.5) решение дифференциального уравнения (1.1) будет даваться формулой (1.6) [10, 11, 12]:
,
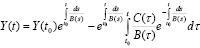Очевидно, (1.6) является обобщением (1.3).
Искомая задача оптимизации потребления ставится, как максимизация интегральной дисконтированной полезности потребления [5]:
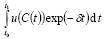, (1.7)
где u – функция полезности, а ? – коэффициент дисконтирования будущей полезности [1].
Вариационный метод решения задачи
Выражая потребление из уравнения (1.1) подставляем его в (1.7):
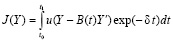. (1.8)
Рассматривается разность J(Y + h) – J(Y), где h = h(t) – малое возмущение и устанавливается не положительность этой разности.
На основании (1.8) записываем (1.9):
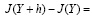
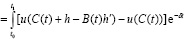dt.
Используя формулу Тейлора с остаточным членом в форме Пеано, имеем
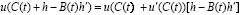
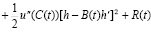, (1.10)
где R(t) = o[h – B(t)h' ]2, при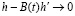 
. (1.11)
Подставляя (1.10) и (1.11) в (1.9), получим (1.12):
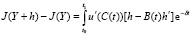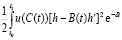dt +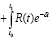 
dt 
dt.
Пользуясь интегрированием по частям, мы можем записать
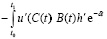dt =
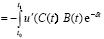dh =
.
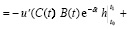
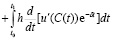Первое слагаемое правой части последнего равенства обращается в нуль, поскольку
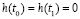. (1.13)
С учетом (1.13) предпоследнее равенство упрощается и будет иметь вид
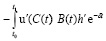dt =
.
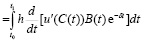Подставляя последнее в (1.12) будем иметь
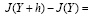
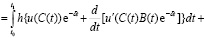
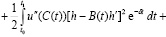
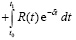. (1.14)
Используя основную лемму вариационного исчисления, будем иметь (1.15):
.
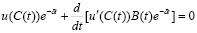С учетом (1.15) представление (1.14) упрощается и будет иметь вид
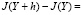
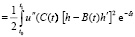dt +
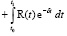. (1.16)
Заметим, что если в (1.16) h заменить на ?h, где b = const, то, т. к. в этом случае h? заменяется на ?h?, можно записать
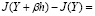
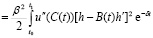dt +
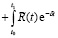dt, (1.17)
где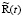 
– остаточный член из формул, аналогичных формулам (1.10), (1.11):
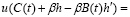
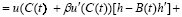
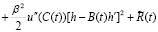, (1.18)
,
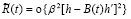при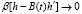 
. (1.19)
Из формул (1.18) и (1.19) следует, что при фиксированном h и b > 0 второе слагаемое правой части (1.17) есть бесконечно малая величина более высокого порядка, чем первое, если только первое слагаемое не равно нулю тождественно. Т. о., знак (1.17) полностью определяется отличным от тождественного нуля первым слагаемым правой части.
Будем считать, что полезность потребления оценивается монотонной функцией u(С), которая описывает относительное отвращение к риску по Эрроу-Пратту [1]. В силу этого u''(C(t)) ? 0, а значит первое слагаемое правой части равенства (1.16) неположительно. Следовательно, в силу (1.16) имеем
,
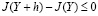а значит (1.6) при (1.15) реализует максимум функционала (1.7), или, что то же самое (1.8) при условиях (1.13).
Особенности вариационного метода решения задачи оптимизации потребления модели экономической динамики Солоу
Модель макроэкономической динамики Солоу весьма популярна и уже стала классической в математической экономике [3, 4, 16]. Уравнение модели макроэкономической динамики Солоу с переменными коэффициентами [3] имеет вид
,
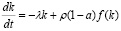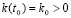. (2.1)
Здесь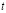 
– время, которое считается непрерывным и измеряется в годах, а 
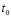– его начальный момент; 
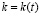– фондовооруженность; 
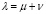, где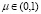 
– доля выбывших за год основных производственных фондов, а 
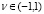– годовой темп прироста числа занятых; 
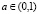– коэффициент прямых затрат (доля промежуточного продукта в валовом общественном продукте); 
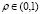– норма накопления ( доля валовых инвестиций в валовом внутреннем продукте; 
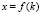– народнохозяйственная производительность труда [3, с. 39-41]. Поскольку, для среднедушевого потребления имеется выражение [3, с. 41]
c = c(t) = (1 – ?)(1 – a)x =
= (1 – ?)(1 – a) f(k) (2.2)
то из (2.2) получаем
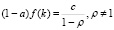. (2.3)
Подставляя (2.3) в (2.1), будем иметь
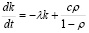. (2.4)
Выражая из (2.4) среднедушевое потребление, получим
, 
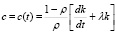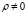. (2.5)
Задача оптимального управления ставится, как максимизация интегральной дисконтированной полезности среднедушевого потребления:
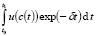, (2.6)
где u – функция полезности, а ? – коэффициент дисконтирования будущей полезности [3, с. 51, 3].
Вариационный метод решения задачи
Обозначив (2.6) за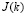 
, получаем функционал, как объект максимизации
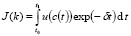. (2.7)
Пользуясь, теперь, выражением (2.5) из (2.7) получим:
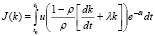. (2.8)
Нам достаточно рассмотреть разность J(k + h) – J(k), где h = h(t) – малое возмущение и показать неположительность этой разности.
На основании (2.8), пользуясь линейностью интеграла, можно записать
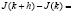
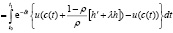. (2.9)
Используя формулу Тейлора с остаточным членом в форме Пеано, имеем
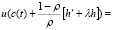
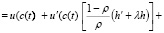
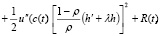(2.10)
где
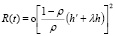(2.11)
при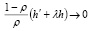 
.
Подставляя (2.10) и (2.11) в (2.9), получим
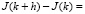
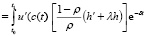dt +
dt +
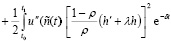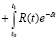dt. (2.12)
Пользуясь интегрированием по частям, мы можем записать
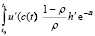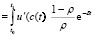dt =
dt =
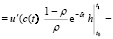
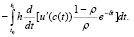(2.12?)
Первое слагаемое правой части последнего равенства обращается в нуль, поскольку
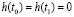. (2.13)
С учетом (2.13) предпоследнее равенство упрощается и будет иметь вид
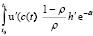dt =
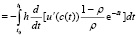.(2.12??)
Подставляя (2.12??) в (2.12) будем иметь
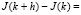
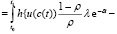
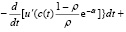
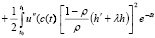dt +
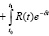dt. (2.14)
Используя основную лемму вариационного исчисления, будем иметь
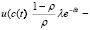
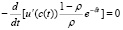. (2.15)
С учетом (2.15) представление (2.14) упрощается и будет иметь вид
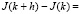
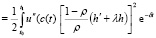dt +
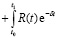dt. (2.16)
Заметим, что если в (2.16) h заменить на ?h, где b = const, то, т. к. в этом случае h? заменяется на ?h?, можно записать
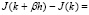
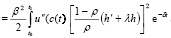dt +
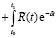dt, (2.17)
где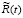 
– остаточный член из формул, аналогичных формулам (2.10), (2.11):
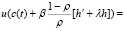
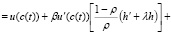
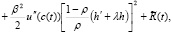(2.18)
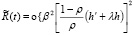(2.19)
при
.
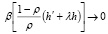Из формул (2.18) и (2.19) следует, что при фиксированном h и b ® 0 второе слагаемое правой части (2.17) есть бесконечно малая величина более высокого порядка, чем первое, если только первое слагаемое не равно нулю тождественно. Т. о., знак (2.17) полностью определяется отличным от тождественного нуля первым слагаемым правой части.
Будем считать, что полезность потребления оценивается монотонной функцией u(c), которая описывает относительное отвращение к риску по Эрроу-Пратту [1]. В силу этого u?(c(t)) ? 0, а значит первое слагаемое правой части равенства (2.16) не положительно. Следовательно, в силу (2.16) имеем
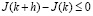, (2.20)
а, значит, в силу (2.20), решение задачи (2.1) [7, 8] с уравнением в форме (2.4) при (2.15) реализует максимум функционала (2.6), или, что то же самое (2.7), при условиях (2.13) [6].
Выводы
В настоящем обзоре приводится и обсуждается вариационный метод решения задач оптимального управления для классических макромоделей экономической динамики. В качестве примеров макромоделей выбраны наиболее популярные: Харрода–Домара и Солоу. В качестве задачи оптимального управления выбрана задача максимизации интегральной дисконтированной модели потребления. Несмотря на то что модели разные, а именно: в случае модели Харрода–Домара уравнение связи допускает хотя и сложное, но точное решение, а в случае модели Солоу задача Коши для уравнения связи лишь эквивалентна интегральному уравнению, предложенный вариационный метод решения достаточно эффективен. В настоящем обзоре рассматривается самый общий случай уравнения связи, когда коэффициенты этого уравнения переменные функции достаточно произвольного характера. Эти случаи рассматриваемых макроэкономических моделей с переменными коэффициентами в уравнениях связи с практической точки зрения гораздо важнее аналогичных решений для задач с постоянными коэффициентами в силу более широкой практической применимости. Однако, эти решения намного сложнее. В настоящем обзоре мы убеждаемся, что для очень важной задачи минимизации интегральной дисконтированной полезности потребления это усиление сложности решений не является непреодолимой помехой для реализации рассматриваемого вариационного метода. Решение задачи будет намного сложнее, однако, оно достаточно успешно реализуется. Трудности, возникающие в результате усиленной постановки, успешно преодолеваются.