Scientific journal

Научное обозрение. Экономические науки

ISSN 2500-3410

ПИ №ФС77-57503

Введение

Функционирование сложных систем порождает необходимость решения проблем их безопасности различного генезиса – социального, экономического, технического, информационного и др. Это объективно связано в первую очередь с возникновением сопутствующих рисков и влечет необходимость решения соответствующих задач – от математического моделирования до разработки систем поддержки принятия решений при управлении рисками сложных систем. Вопросы безопасности сложных социальных, экономических, технических систем являются ключевыми при оценке эффективности их функционирования. Например, для организации, производящей продукцию (товары и/или услуги), вложения в безопасность (в частности, информационную), как нематериальный актив организации, являются фактором ее стратегической стабильности, уменьшая риски критических финансовых потерь в связи с нарушением безопасности функционирования, что, по сути, превращает указанные вложения в инвестиционные и делает актуальной тему данной статьи.

В настоящее время опубликовано значительное количество работ, касающихся вопросов моделирования защищенности (экономической, информационной, технологической и др.) различных систем функционирования организации, большинство из которых в первую очередь рассматривают аспект информационной безопасности (ИБ). В работе [1] описывается современное состояние проблемы обеспечения, контроля и информационной защищенности в эргасистемах, как сложных системах управления объектами технических, технологических, организационных, экономических комплексов, имеющих существенный признак обязательного наличия человеческого или социального фактора в них. В монографии [2, с. 45–74] обоснована целесообразность использования методов исследования операций в системах управления ИБ, предложены возможные области применения моделей и методов комплексного управления информационной защитой объектов информатизации. Экономический аспект учета рисков ИБ организации рассматривается в работе [3]. Статьи [4; 5] посвящены анализу основных подходов к определению оптимального объема инвестиций, необходимого для обеспечения информационной безопасности информационной системы в рамках математической модели Гордона – Лоеба, в которой рассмотрены затраты на предотвращение угроз ИБ. В работе [6] акцентирована необходимость рассмотрения потоков затрат на компенсацию ущерба, возникающего при реализации угроз ИБ. В современных научных трудах по математическому моделированию задач информационной безопасности информационных систем организаций рассматриваются различные аналитические методы. В работе [7] использованы методы теории графов, а в [8] – теоретико-информационный метод энтропийно-вероятностного анализа дерева событий. В работах [9; 10] применены модели многокритериальной и дискретной оптимизации соответственно. В основу указанных методов чаще всего положен вероятностный принцип оценки рисков ИБ, в настоящее время подвергающийся обоснованной критике в литературе (например, [11]). Кроме того, среди описываемых моделей, алгоритмов и методов решения задачи оценки уровня информационной защищенности информационной системы организации (ИЗИСО) редко встречаются легко интерпретируемые, понятные практикам оптимизационные модели, для которых разработаны эффективные средства их автоматизированного анализа, наличие которых является необходимым условием разработки систем поддержки принятия решений в задачах управления ИЗИСО.

Цель исследования – построение двухкритериальной математической модели оценки уровня информационной защищенности информационной системы организации для определения оптимального распределения инвестиционного ресурса, включающего как потоки затрат, ориентированные на предотвращение угроз, так и потоки затрат на компенсацию возникающего ущерба от реализации угроз безопасности.

Материалы и методы исследования

Пусть изучаемая сложная система представляет собой информационную систему организации (ИСО). Очевидно, что информационная защищенность ИСО тем выше, чем ниже риски реализации различных угроз ее функционированию – нарушения работы электронных сред контроля систем управления, технологических цепочек, документооборота; отказов работоспособности аппаратного, программного обеспечения ИСО, связанных с внешним вмешательством или недостаточной квалификацией сотрудников, управленцев и др. При этом безопасность (в том числе информационная) сложной системы определяется не только мерами по предотвращению ее угроз, но и мерами по нейтрализации возможного ущерба в случае реализации этих угроз. Поэтому общий уровень ИЗИСО определяется минимумом суммы рисков предупреждения угроз безопасности и рисков компенсации ущерба, возникшего в связи с реализацией этих угроз, что соответствует использованию принципа минимакса, заключающегося в минимизации интегрального ущерба, который лицо, принимающее решения (ЛПР), не может предотвратить при развитии событий по наихудшим для него сценариям. Это требует рассмотрения как минимум двух критериев при решении задач ИЗИСО.

В связи со сказанным, в отличие от однокритериальной модели работы [12], где были рассмотрены риски ИСО от угроз до их реализации (априорные угрозы), здесь рассмотрим еще и риски, возникающие в связи с реализацией апостериорных угроз ИЗИСО. В отличие от использованной в однокритериальной модели обратно пропорциональной линейной зависимости риска r1~а1–b1·х от затрат (инвестиций) х, выделенных на предотвращение априорных угроз, для целей купирования апостериорных угроз используем зависимость, имеющую прямую пропорцию связи риска r2 функционирования ИСО с затратами y на компенсацию ущерба: r2~а2+b2·y. Иначе говоря, предполагается, что суммарный риск ИЗИСО на обеих стадиях функционирования ИСО понижается, если увеличивается сумма затрат на избежание угроз и компенсацию ущерба от реализации угроз (рисков), что соответствует росту ИЗИСО. Заметим, что коэффициент а1 может трактоваться как максимальный объем затрат, который понадобится в случае реализации угроз при отсутствии инвестиций в купирование априорных угроз, а коэффициент а2 – как минимальный объем затрат, который будет необходим для компенсации ущерба ИСО при отсутствии инвестиций в купирование апостериорных угроз. Минимальную сумму затрат x на защиту (избежание, устранение, уменьшение) от априорных угроз и затрат y на компенсацию (избежание, устранение, уменьшение) ущерба от апостериорных угроз будем считать оптимумом (максимальным уровнем) ИЗИСО. При этом оптимальные общие затраты должны соответствовать равенству x = y, которое становится очевидным при использовании нелинейных зависимостей уровня ИЗИСО от осуществляемых затрат x и y, в случае их противоположной монотонной направленности (например, [6, c. 52]). Следует отметить, что для универсальной организации, вообще говоря, трудно разделить бюджеты затрат на защиту от априорных угроз и на компенсацию ущерба от апостериорных угроз, вследствие чего целесообразно рассмотреть дополнительный управляющий параметр α, учитывающий соотношение оптимальных инвестиций x и y. Для производственной организации, производящей товары и/или услуги, гибкость управления ИЗИСО будет обусловлена соотношениями бюджетов общих затрат, затрат на защиту от априорных угроз, на компенсацию ущерба от апостериорных угроз, а также диапазонами выделяемых средств на купирование каждой угрозы в отдельности. Указанные соотношения могут иметь многочисленные варианты в зависимости от структуры менеджмента организации и его отношения к рискам безопасности.

Рассмотрим следующую математическую модель информационной защищенности информационной системы организации. Пусть N – количество априорных угроз ИБ, а L – количество видов ущерба ИС, соответствующих апостериорным угрозам ИБ;

xk (k = 1, …, N) – инвестиции в предотвращение k-й угрозы ИБ, денежных единиц (д.е.);

xN+l (l = 1, …, L) – затраты на устранение (N+l)-го ущерба, д.е.;

(b1)k (k = 1, …, N) – весовые коэффициенты значимости k-й угрозы ИБ;

(b2)l (l = 1, …, L) – весовые коэффициенты значимости l-го ущерба ИБ;

Z – общий бюджет на обеспечение ИЗИСО, д.е.;

Z1 – бюджет на предупредительные мероприятия по обеспечению ИЗИСО, д.е.;

Z2 – бюджет на мероприятия по компенсации ущерба в связи с нарушениями ИЗИСО, д.е.;

α – коэффициент соотношения суммарных затрат на предупредительные мероприятия (априорные угрозы) и суммарных затрат на мероприятия по компенсацию ущерба (апостериорные угрозы).

Тогда математическая модель ИЗИСО принимает следующий вид:

Критерии эффективности ИЗИСО

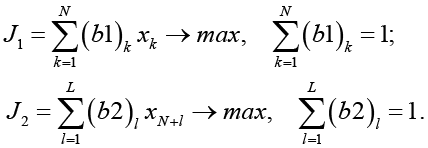
(1)

Ограничения финансирования ИЗИСО:

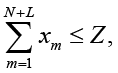
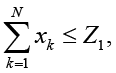
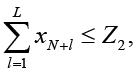
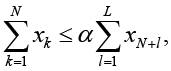
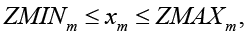
xm ≥ 0, m = 1, …, N+L. (2)

Результаты исследования и их обсуждение

Модель (1)–(2) обобщает модель в [12] на случай рассмотрения двух типов затрат на обеспечение ИЗИСО – на предупредительные мероприятия до и на компенсацию ущерба после реализации угроз ИБ. Путем замены переменных ym = xm – ZMINm задачу (1)–(2) можно привести к эквивалентной задаче, содержащей нулевое решение, что, учитывая компактность допустимого множества, позволяет доказать существование решения для любого набора параметров задачи. Кроме того, учитывая линейность модели, ее можно свести к эквивалентной ей, однокритериальной задаче с выпуклой линейной сверткой критериев:

J = μJ1+(1-μ)J2, μ ? (0;1),

где μ – экспертно задаваемый весовой коэффициент значимости критериев. Нетривиальные решения (1)–(2) получаются с помощью оптимизационного пакета, описанного в [13, с. 96–111]. Принятие решений по распределению инвестиций и оценке уровня ИЗИСО может основываться как на изучении зависимостей от параметра μ, так и на анализе получаемого Парето-множества модели, автоматизированные средства которого также содержатся в указанном оптимизационном пакете. Отметим, что представленную математическую модель ИЗИСО, вообще говоря, можно использовать как основу для поддержки обоснованных решений не только в сфере информационной безопасности, но и для решения задач комплексной безопасности сложных систем, по аналогии с тем, как это сделано в работах [14; 15] относительно системы поддержки принятия решений при оценке информационно-экономической безопасности организации. Для проверки работоспособности модели (1)–(2) проведем модельный вычислительный эксперимент.

Пусть имеются следующие значения входных параметров модели (1)–(2):

N = L = 2; Z = 1300 д.е., Z1 = 800 д.е.,

Z2 = 900 д.е.; (b1)1 = 0,55, (b1)2 = 0,45;

(b2)1 = 0,4, (b2)2 = 0,6; ZMAX1 = 700 д.е.,

ZMAX1 = 1500 д.е., ZMAX3 = 300 д.е.,

ZMAX4 = 400 д.е., ZMIN1-4 = 0 д.е.

Произведем расчеты при заданных входных значениях и построим графики зависимостей J(μ), придавая параметру α значения 0; 0,5; 1; 1,5; 2 (рис. 1).

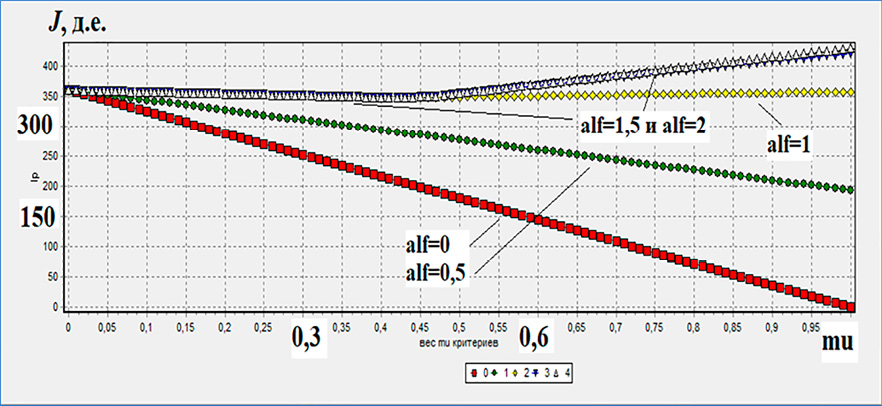
Рис. 1. Зависимости J(μ) Примечание: составлен авторами по результатам исследования

Оптимальные решения и значения свертки критериев J

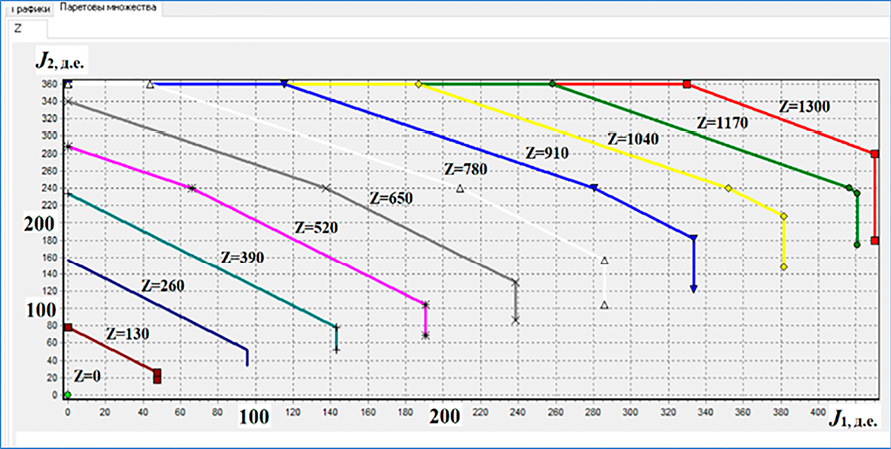
Рис. 2. Парето-множества по параметру Z при α = 2 Примечание: составлен авторами по результатам исследования

Отметим, что зависимости J(μ) совпадают при α = 1,5 и α = 2. Приведенные на рис. 1 данные свидетельствуют о нетривиальной зависимости уровня ИЗИСО по модели (1)–(2) от значений параметра α даже при небольшом количестве рассматриваемых априорных и апостериорных угроз ИБ, что, безусловно, требует дальнейшего изучения свойств и многопараметрического анализа построенной модели. В таблице приведены также оптимальные решения и соответствующие значения свертки J критериев задачи при μ = 0,5.

Как видно из таблицы, полученные оптимальные решения существенно определяются значениями параметра α и соответствуют содержательному смыслу решаемой задачи. Построим далее Парето-множества задачи (1)–(2) в зависимости от изменения параметра общих затрат Z в диапазоне от 0 до 1300 д.е. с шагом 130 д.е. и α = 2 (рис. 2).

На рис. 2 изображены Парето-множества задачи (1)–(2), причем по осям координат отложены значения каждого из критериев. Используя полученные данные, аналитик ИБ или любое другое ЛПР может определить оптимальные диапазоны изменения значений критериев J1 и J2 эффективности затрат на купирование априорных и апостериорных угроз ИБ. Так, например, при Z = 130 – J1?(0;48), J2?(20;80), при Z = 780 – J1?(0;285), J2?(100;350), а при Z = 1300 – J1?(0;550), J2?(180;355).

Заключение

Математическая модель (1)–(2) представляет собой легко интерпретируемую для использования специалистами-практиками, имеющую экономический смысл оптимального распределения ресурсов задачу линейного программирования в стандартной форме. Для ее предварительного анализа автор использовал решающий указанную задачу многопараметрический графоанализатор с возможностями графического и Парето-анализа. Совокупность данных инструментов позволяет реализовать принцип информационной, модельной и алгоритмической сбалансированности, практически необходимый для разработки эффективных автоматизированных систем поддержки принятия решений в условиях значительного количества угроз безопасности функционирования сложных систем. Благодаря идентичности подходов к оценке рисков функционирования сложных систем путем рассмотрения взвешенной комбинации затрат на мероприятия по нивелированию (снижению, устранению, уменьшению, компенсации и пр.) рисков в любой сфере человеческой деятельности, построенная в работе модель может быть применена для оценки оптимальных затрат на защиту от угроз безопасности и тем самым для повышения уровня общей безопасности в социальных, экономических, технических, информационных и других сложных системах.